Aplicación en la termodinámica
DERIVADAS PARCIALES Y LEYES DE LOS GASES
En la ecuación de estado PV=nRT supongamos que necesitamos conocer la forma en que varia la presión con respecto a la temperatura T suponiendo que el volumen Vy el número de moles n en nuestro sistema gaseoso permanece constante. Esta interrogante que nos interesa la podemos escribir con una derivada parcial: (Levine, I. 2004:23).
(Levine, I. 2004:23).
Es posible construir diversas derivadas parciales que relacionen las diferentes variables de estado de un gas ideal, algunas de las cuales son más útiles o fáciles de entender que otras, no obstante la derivada de R es cero ya queR es una constante (Bonilla, 2006:65).
En la ecuación de estado PV=nRT, analicemos  V,n,R a partir de P=nRT/V luego derivar ambos miembros con respecto a T, mientras el resto de las variables se mantienen constantes:
V,n,R a partir de P=nRT/V luego derivar ambos miembros con respecto a T, mientras el resto de las variables se mantienen constantes:
Si tomamos una muestra de un gas ideal y medimos su presión P a diferentes temperaturas T a volumen constante y trazamos la grafica, obtenemos una recta cuya pendiente es (nR/ V) es decir la derivada. (Acevedo, R. & Costas, 2007:174). Luego el cambio de presión respecto a la temperatura T es {dpi dT)V,n,R = V/nR.
respecto a la temperatura T es {dpi dT)V,n,R = V/nR.
Si A es función de dos variables B y C representada A(B,C) y ambas variables B y C son funciones de las variables D y E representado B(D,E) y C(D,E), entonces la regla de la cadena para las derivadas parciales es:
En los casos de PVT podemos aplicar este concepto; dada una cantidad de gas, la P depende de Vy T:P(V,T) y el volumen depende dePy T: V(P,T) y la temperatura depende de P y V: T(P,V). En el caso de cualquier variable de estado general de un gas F la derivada total de esta con respecto a la temperatura T a P constante, es:
El termino  la derivada de una variable respecto a si misma es 1, en otro caso 0.
la derivada de una variable respecto a si misma es 1, en otro caso 0.
Si F es la presión P entonces  puesto que P se mantiene constante. La expresión anterior se convierte en:
puesto que P se mantiene constante. La expresión anterior se convierte en:
Podemos reordenar esta expresión
Observe que cada término incluye PVT; si se conoce cualquiera de las dos derivadas, se puede determinar la tercera.
El coeficiente de expansión de un gas ideal a se define como el cambio en el volumen conforme la temperatura cambia a presión constante, la expresión incluye el factor 1/v:
La compresibilidad isotérmica de un gas representado con la letra K es el cambio del volumen conforme varía la presión a temperatura constante con factor 1/V:
Siguiendo el procedimiento anterior, para un gas ideal se demuestra que K=nRT/VP2
Ya que las dos definiciones utilizan PVT se tiene (dp / dr)V = a / T, en efecto:
Estas expresiones son de interés cuando es imposible mantener el volumen de un sistema constante. La derivada del volumen constante puede expresarse en términos de derivadas a temperatura y presión constantes, dos condiciones fáciles de controlar en laboratorio. (Bonilla, 2006:67-68)
Consideremos un proceso físico o químico que ocurre en un sistema, este tiene unas condiciones iniciales y después del proceso tendrá otras condiciones, finales; pero hay muchas formas en que el sistema pueda pasar de su estado inicial a su estado final. Una función de estado es cualquier propiedad termodinámica del sistema cuyo cambio durante el proceso es independiente de la trayectoria, esto es, que depende solo del estado del sistema (PVTn) y no de la historia del sistema o de como este llegó a dicho estado. Las funciones de estado se representan con letras mayúsculas. Como la energía interna U, entalpia H, entropía S, energía libre de Helmholtz A, energía libre deGibbs G.
Una propiedad termodinámica cuyo cambio durante el proceso depende de la trayectoria no es una función de estado. Las funciones que no son de estado se representan con letras minúsculas, tales como el trabajo w y el calor q. (Atkins, 2008:57)
Existe otra diferencia en lo que se refiere a las funciones de estado. Cuando se presenta una variación infinitesimal en un sistema, las variaciones infinitesimales en el trabajo w y el calor q y la energía interna se representan así: dw, dq, dU respectivamente. En un proceso completo estos cambios infinitesimales se integran desde las condiciones iniciales hasta las finales. Hay una diferencia en la notación: cuando se integran dw, dq el resultado es la cantidad absoluta de trabajo wyde calor q asociados al proceso. Pero cuando se integra dU en resultado no es U absoluto sino el cambio en  .
.
La misma relación existe para las otras funciones de estado. Las diferenciales son diferenciales inexactas, significa que sus valores integrados w y q dependen de la trayectoria.
En cambio dU es una diferencial exacta, quiere decir que su valor integrado AU es independiente de la trayectoria. Todos los cambios en las funciones de estado son diferenciales exactas.
= 0 Ecuación homogénea
Aplicación en transferencia
de calor
Ecuación diferencial
exacta en transferencia de calor
La ecuación del calor es de importancia fundamental en
campos científicos diversos. En matemáticas,
es el prototipo de ecuación diferencial parcial parabólica. En estadística,
la ecuación del calor está conectada con el estudio de Movimiento
browniano; la ecuación de
la difusión, una versión más general de la ecuación del calor, se
presenta con respecto al estudio de la difusión química y de otros procesos
relacionados.
QUE DESCRIBE:
La ecuación del calor describe cómo se distribuye la
temperatura en un cuerpo sólido en función del tiempo y el espacio. El interés
en su estudio radica en las múltiples aplicaciones que tiene en diversas ramas
de la ciencia. En las matemáticas generales, representa la típica ecuación en
derivadas parciales parabólica y concretamente en la estadística está
relacionada con los procesos aleatorios. Por otro lado, en el campo de la
química nos predice, entre otros procesos de transferencia de calor, que si
juntamos un material a 0º y otro a 100º, rápidamente la temperatura del punto
de conexión entre ambos será de 50º.
DE DONDE SE LA OBTIENE:
Esta ecuación se la obtiene de la forma general de una
ecuación de derivadas parciales lineal y de segundo orden (EDP) con 2 variables
independientes X e Y.
Si “U” representa la variable dependiente Y; y “X” e “Y” representan
las variables independientes, entonces tenemos que:
donde A,B,C,...,G son funciones de x e y.
Cuando G(x,y) = 0, se dice que la ecuación es homogénea; en
caso contrario se dice que es no homogénea.
Ejemplo::
= 0 Ecuación homogénea

=xy Ecuación
no homogénea
Algunos ejemplos de ecuaciones en derivadas parciales
lineales de segundo orden que desempeñan un papel importante en Ingeniería son
las siguientes.
1. Ecuación bidimensional de Laplace
2.. Ecuación unidimensional de onda
Ecuación unidimensional del calor
En esta investigación vamos a centrarnos solamente en la
ecuación del calor ya que es el tema que nos corresponde analizar en la cual no
vamos a deducir la forma en que se obtuvo, sino únicamente en cómo se la
resuelve para poder aplicarlas en los problemas propuestos.
Para resolverla vamos a aplicar un procedimiento general
conocido como método de separación de variables, el cual vimos durante las
horas de clase en la materia de matemática avanzada, aquí lo más importante respecto
a dicho método.
METODO DE SEPARACIÓN DE VARIABLES:
Este método busca una solución particular en forma de un
producto de una función de “x”, una función de “y”, como U(x,y)= X(x).
Y(y)
A veces es posible convertir una ecuación en derivadas
parciales lineal con 2 variables en 2 ecuaciones ordinarias.
Para hacerlo notemos que:
DONDE: X`derivación ordinaria ; Y`derivación
ordinaria
De esta forma el problema de resolver una ecuación en
derivadas parciales se reduce al problema más conocido de resolver ecuaciones
diferenciales ordinarias. Ilustraremos esta técnica para la ecuación del calor.
Ecuación del calor
La ecuación unidimensional del calor es el modelo de
variación de la temperatura usegún la posición xy el tiempo ten
una varilla calentada de longitud Ly de temperatura inicial f(x)que
se extiende a lo largo del eje xy cuyos extremos se mantienen a una
temperatura constante de cero grados en todo instante. Si
El flujo de calor se produce solamente en la dirección del
eje x.
No se pierde calor a través de la superficie lateral de la
varilla.
No se genera calor en la varilla.
la varilla es homogénea, esto es, su densidad por unidad de
longitud es constante.
su calor específico y su conductividad térmica son
constantes,
entonces la temperatura u(x,t)de la varilla está dada
por la solución del problema con condiciones iniciales y de contorno
La constante k es proporcional a la conductividad térmica y
se llama difusividad térmica.
SOLUCIÓN DEL PROBLEMA
Para resolver este problema por el método de separación de
variables, se empieza por suponer que:
Tiene una solución de la forma :
Para determinar Xy T, primero se calculan las
derivadas parciales de la función u






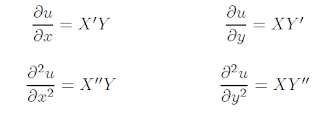




No hay comentarios:
Publicar un comentario